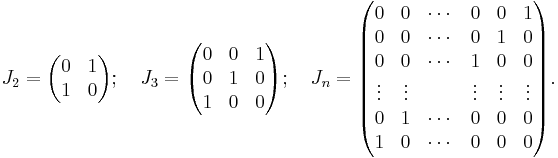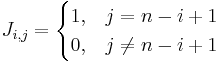Exchange matrix

In mathematics, especially linear algebra, the exchange matrix is a special case of a permutation matrix, where the 1 elements reside on the counterdiagonal and all other elements are zero. In other words, it is a 'row-reversed' or 'column-reversed' version of the identity matrix.

$J_{2}=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix};\quad J_{3}=\begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{pmatrix}; \quad J_{n}=\begin{pmatrix} 0 & 0 & \cdots & 0 & 0 & 1 \\ 0 & 0 & \cdots & 0 & 1 & 0 \\ 0 & 0 & \cdots & 1 & 0 & 0 \\ \vdots & \vdots & & \vdots & \vdots & \vdots \\ 0 & 1 & \cdots & 0 & 0 & 0 \\ 1 & 0 & \cdots & 0 & 0 & 0 \end{pmatrix}.$

Definition

If J is an n×n exchange matrix, then the elements of J are defined such that:

$J_{i,j} = \begin{cases} 1, & j = n - i %2B 1 \\ 0, & j \ne n - i %2B 1\\ \end{cases}$

Properties

J^T = J.
Jⁿ = I for even n; Jⁿ = J for odd n, where n is any integer. Thus J is an involutary matrix; that is, J⁻¹ = J.
The trace of J is 1 if n is odd, and 0 if n is even.

Relationships

Any matrix A satisfying the condition AJ = JA is said to be centrosymmetric.
Any matrix A satisfying the condition AJ = JA^T is said to be persymmetric.